concepto de limite En matemática, el límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. El límite de una función es un concepto fundamental del cálculo diferencial matemático.

Informalmente, el hecho que una función f tiene un límite L en el punto p, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente cercanos a p, pero distintos de p.

En análisis real para funciones de una variable, se puede hacer una definición de límite similar a la de límite de una sucesión, en la cual, los valores que toma la función dentro de un intervalo se van aproximando a un punto fijado c, independientemente de que éste pertenezca al dominio de la función. Esto se puede generalizar aún más a funciones de varias variables o funciones en distintos espacios métricos.
Informalmente, se dice que el límite de la función f(x) es L cuando x tiende a c, y se escribe:
si se puede encontrar para cada ocasión un x suficientemente cerca de c tal que el valor de f(x) sea tan próximo a L como se desee.
Para un mayor rigor matemático se utiliza la definición épsilon-delta de límite, que es más estricta y convierte al límite en una gran herramienta del análisis real. Su definición es la siguiente:

"El límite de f(x) cuando x tiende a c es igual a L si y sólo si para todo número real ε mayor que cero existe un número real δmayor que cero tal que si la distancia entre x y c es menor que δ, entonces la distancia entre la imagen de x y L es menor que εunidades".

limite de una función 

El límite de una función real de variable real es un concepto fundamental del análisis matemáticos , un caso de límite que se aplica a otros conceptos de suma importancia como derivada o integral, más aún a las funciones de variable compleja.

Intuitivamente, el hecho que una función f alcance un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente próximos a c, sin importar el valor que pudiera adquirir f en el punto c.

Si la función tiene límite en podemos decir de manera informal que la función tiende hacia el límite cerca de si se puede hacer que esté tan cerca como queramos de haciendo que esté suficientemente cerca de siendo distinto de .
Los conceptos cerca y suficientemente cerca son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice:

El límite de una función f(x), cuando x tiende a c es L si y sólo si para todo existe un 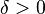tal que para todo número real x en el dominio de la función .

limites 

límites 

LÍMITES FUNCIONES A TROZOS (FUNCIONES POR PARTES) Las funciones a trozos también son conocidas como funciones definidas por partes o funciones determinadas por más de una ecuación. En este ensayo vamos a ver varios ejercicios resueltos de límites para funciones de esta categoría. Instrucciones: Para cada una de las siguientes funciones definidas por partes (funciones a trozos) trazar la gráfica y determinar los siguientes límites (si existen). Límite por la izquierda cuando x tiende a 1 lim → Límite por la derecha cuando x tiende a 1 lim → Por definición, el límite como tal (sin aclarar por la izquierda o por la derecha) existe si y solo si se cumple la existencia del límite por la izquierda, el límite por la derecha y si ambos son iguales. lim → Recuerda que vamos a buscar estos tres límites para cada una de las funciones que se presentan a continuación. Para facilitar la comprensión las gráficas se realizaron mediante software graficador ya que nuestro objetivo no es ver cómo se grafica cada función sino analizar el comportamiento en las inmediaciones del valor = 1. Si es obligatorio para ti graficar “a mano” o simplemente lo haces por pasatiempo, recuerda realizar una tabla de valores asignando valores a “x” y sustituyendo según corresponda en cada función, para encontrar los valores correspondientes de y, para ello es aconsejable que asignes a x los valores inmediatamente cercanos al valor crítico = 1, tanto por la izquierda (es decir, valores decimales muy cercanos a 1 que estén entre 0 y 1 como 0, 0.2, 0.4, 0.6, 0.8) y valores por la derecha (es decir, valores decimales muy cercanos a 1 que estén entre 1 y 2 como 2, 1.8, 1.6, 1.4, 1.2) de esa forma obtendrás una aproximación numérica al límite por la izquierda y por la derecha para cada función. Antes que nada recuerda un concepto muy importante: un límite es siempre un valor al que se aproxima la variable y. Es un valor de y, no de x. http://CursoDeCalculo.com Profesor Raúl Vega Muñoz = + 1 < 1 1 = 1 + 1 > 1 La gráfica de la función es la que se muestra en seguida: Observamos que en el intervalo −∞, 1 la gráfica de es similar a una parábola, obedeciendo la ecuación cuadrática que determina esa región de la curva, pero la gráfica se interrumpe en el valor = 1. Justamente en el valor = 1 la gráfica corresponede a la recta horizontal = 1, pero como solo está definida para ese único valor, en vez de ver una recta vemos solamente un punto: el punto 1,1 . Finalmente en el intervalo 1, ∞ la gráfica es similar a la recta oblícua = + 1. Podemos apreciar que los cambios más importantes desde el punto de vista gráfico ocurren en el valor = 1 y sus inmediaciones. Calculamos el límite cuando x tiende a 1 por la izquierda. lim → Podemos apreciar que a medida que los valores de se aproximan a = 1 desde la izquierda, los valores de y se aproximan a 2. Nota que no nos interesa el valor de la función en = 1 Concluimos que lim → = 2 De forma análoga, podemos calcular el límite por la derecha.